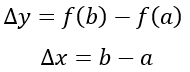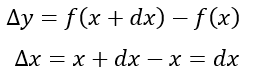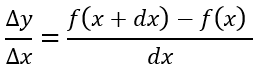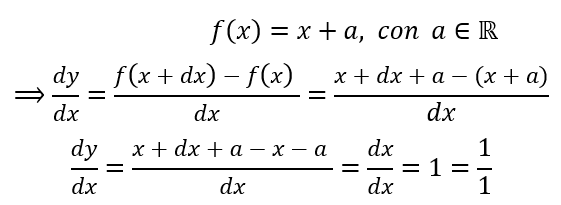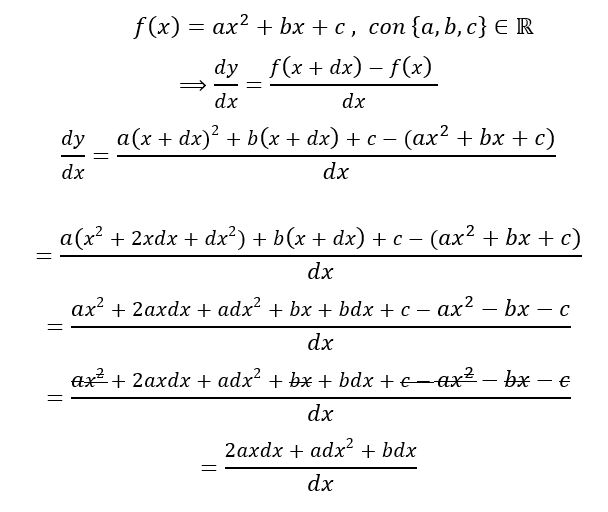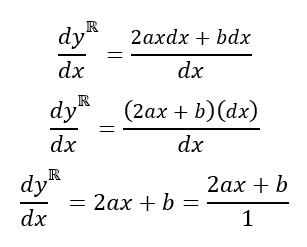Ecuaciones simétricas de una recta.

Dada una recta L en el espacio definida por dos puntos de los cuales uno de ellos es conocido; además se conoce que es paralela a un vector V que se ubica en el espacio, como se muestra en la siguiente figura:

Imagen 1: Recta en el espacio paralela a V.

Entonces es posible conocer las ecuaciones simétricas de la recta las cuales parten y se desarrollan a partir del siguiente raciocinio:

Si L//V entonces en L existirán dos puntos cualesquiera sobre la recta tales que PP1//V, es decir que se pueda formar sobre la recta un vector paralelo a V. Además si multiplicamos a cualquiera de los dos vectores por un parámetro "t" es posible establecer una igualdad entre los dos vectores; así se tendría: PP1=tV, este parámetro "t" permitirá aumentar o reducir el tamaño de V, para que sea igual en tamaño, dirección y sentido que el vector formado sobre la recta L. A continuación se muestra con números lo dicho:

 Sea P1=(x1,y1,z1) ^ P=(x,y,z), donde P1 ^ P son dos puntos sobre L y donde P1 es un punto conocido y P uno desconocido pero que se sabe que está sobre la recta. Además, el vector V=(a,b,c); donde {a,b,c} pertenecen a los reales. Si formamos un vector paralelo a V sobre la recta con misma dirección y sentido se tendría:

PP1= (x-x1,y-y1,z-z1)

Ahora  bien, si igualamos el vector PP1 con V por medio del parámetro t, se tendría:

PP1=tV

(x-x1,y-y1,z-z1)=t(a,b,c); con t perteneciente a los reales.

 (x-x1,y-y1,z-z1)=(ta,tb,tc)

 Ahora bien, t será el parámetro tal que permitirá enunciar la siguiente igualdad:

x-x1=ta   ---1

y-y1=tb   ---2

z-z1=tc   ---3

 Si de las tres ecuaciones despejamos a t, se tendrá:

Dado que en los tres casos el parámetro "t" es el mismo, es posible igualar estas tres ecuaciones, formando así las ecuaciones simétricas de una recta en el espacio.

Imagen 2: ecuaciones simétricas de una recta en el espacio.

 

Bibliografía.

Fuller, Gordon. (2001). Geometría Analítica. México.  CECSA, 5th edición. Pp. 309-310.

Definición de derivada de una función.

Se recomienda que el lector tenga claro los significados de "Función real de variable real",  "Diferencial", "números hiperreales" y "números infinitesimales de "n" orden" para una mejor comprensión de este texto; los cuales podrá consultar haciendo clic en los siguientes enlaces y en los textos recomendados en la bibliografía:

=> Diferencial 

=> Función

 Dependiendo del campo de estudio en que se utilice la derivada, esta puede tener distintas connotaciones como lo son: la velocidad de un móvil, la pendiente de una curva, la rapidez de un móvil, etc...

Ismael Arcos Quezada menciona en su libro: "...la derivada de una función real en una variable es una razón de cambio, la medida del cambio de la función correspondiente a un cambio unitario en el valor de la variable" (1)

Se menciona que la derivada de una función real en una variable es una razón de cambio; pero ¿qué es una razón de cambio?

Definición 1. Se llama razón de cambio al cociente de dos incrementos tanto en la variable independiente como en la dependiente de la función.

De esta forma; sea y=f(x) en donde "x" será la variable independiente y "y" la dependiente; si existe un incremento (2) en "x" por consiguiente también lo existirá en "y"; entonces se podrá expresar la razón de cambio de la siguiente forma:

Sea un punto P1(a, f(a)) que habita sobre la curva y=f(x); se desea saber el incremento en ambas variables cuando x=b, con a y b pertenecientes a los reales. Entonces, existirá un punto P2(b,f(b)) sobre la curva y sus respectivos incrementos en cada una de las variables será:

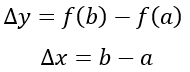Imagen 1: Incrementos en ambas variables.

Supongamos que si se quiere determinar un incremento infinitesimal, denotando dicho incremento con el par de letras "dx" correspondiente para la variable independiente y "dy" correspondiente para la variable dependiente, se tendrá:

Sea ahora el punto inicial P1(x, f(x)) y P2 (x+dx, f(x+dx)), donde "dx" será una cantidad infinitamente pequeña: 

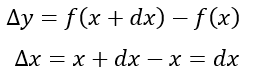Imagen 2: Incremento en cada una de las variables involucrando un infinitesimal.

 Si expresamos estos incrementos como una razón de cambio, tendríamos:

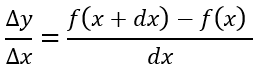Imagen 3: Razón de cambio de dos incrementos

Ahora bien, dado que una función real de variable real que es derivable sobre un intervalo I tiene que ser continua a lo largo de dicho intervalo, entonces es posible dictaminar que el incremento que se produzca sobre la variable dependiente también será infinitesimal; si dicho incremento infinitesimal lo expresamos con la letra "d", entonces la razón de cambio quedará expresada como:

Imagen 4: Derivada de una función.

Entiéndase por esta expresión como la razón de cambio de dos incrementos infinitesimales.

Para comprender mejor el concepto de derivada y lo que está sucediendo en una función real de variable real cuando se deriva, se propondrá la siguiente función y se procederá a derivarla:

Sea:

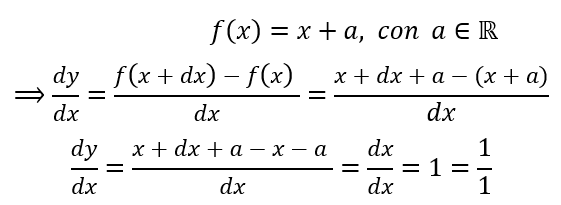Imagen 5: Derivada de una recta en el plano.

 Como puede observase, la derivada de una función de variable real que es continua en un intervalo I, puede entenderse y visualizarse como la razón del cambio existente en la variable dependiente (numerador) por un cambio unitario de la variable independiente (denominador). Esto es debido a que, como ya habíamos visto y desarrollado, la derivada es una razón de cambio de dos incrementos efectuados tanto en la variable dependiente como independiente (ver imagen 2 y 3), por ello el resultado de la derivada puede entenderse como la medida del cambio existente en la función dado un incremento infinitesimal por un cambio unitario en la variable independiente.

Realizaremos un último ejemplo con una parábola con eje focal vertical o directriz horizontal.

Sea:

 

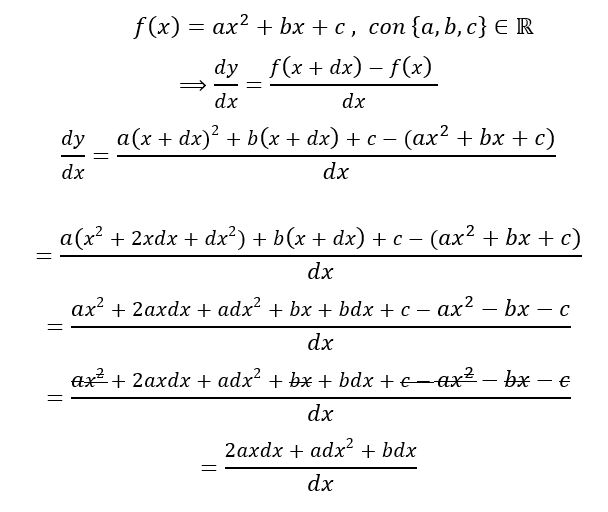Imagen 6: Proceso de derivación de una función cuadrática.

Dado que en la imagen 6 se arroja un infinitesimal de segundo orden, será necesario separar aquellas cantidades que pertenecen al conjunto numérico de los números reales de aquellos números que son hiperreales. Para realizar esta separación, utilizaremos la notación propuesta por Alfredo Jiménez Colín (3). De esta forma, si queremos visualizar la expresión resultante únicamente en su parte real, tendríamos:

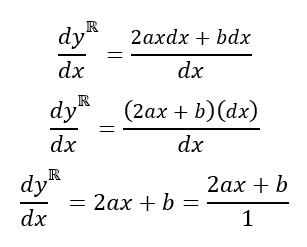Imagen 7: Derivada de una parábola con eje focal vertical.

 Nuevamente es posible visualizar el resultado como una razón de cambio resultante en la variable dependiente por un cambio unitario en la variable independiente.

Referencias.

(1) Arcos Quezada, José Ismael. Cálculo 2 para estudiantes de ingeniería. Editorial Kali. 4ta edición. Toluca, México. 2022. pág. 7. 

(3) Jiménez Colín, Alfredo. (2021). Propuesta de representación simbólica de operaciones con infinitesimales. Revista Educere, Número 82, 825-839. Recuperado de: Propuesta de representación simbólica de operaciones con infinitesimales.

 Notas.

(2) Entiéndase por incremento al aumento longitudinal que se tiene en cada uno de los elementos de la coordenada después de ser valuada en sus valores original y final de la función. (Ver concepto de Diferencial)

Bibliografía.

(4) Ely, Robert. (2010). Nonstandard Student Conceptions About Infinitesimals. Journal for Research in Mathematics Education, 117-146.

(5) Selem Ávila, Elías. (1997). n-extensiones propias de *R de cardinales Nn. Aportaciones matemáticas, 13-24.

¿Puede una matriz con más columnas que filas generar Rm?

Respuesta: Sea una matriz A de dimensión mxn con m<n, entonces esta matriz posee la característica de tener más columnas que filas, por tanto la respuesta es sí. La justificación se presenta a continuación:

Téngase en consideración una matriz A de dimensión 2x3 cuya configuración general se muestra a continuación:

Matriz general 2x3.

 

Por tanto, la matriz aumentada quedará representada como:

Matriz general 2x3 aumentada.

 Como el vector que se aumentó a la matriz A tiene dos componentes (b1 y b2), querrá decir que se procederá a evaluar si las columnas de A pueden generar R2, para ello será necesario determinar la matriz reducida de A aumentada.

Siempre y cuando la matriz presente una consistencia, podrán producirse los siguientes dos casos:

Caso I:

Matriz aumentada general en caso I.

Recordemos que el símbolo (*) significa que dicha entrada tiene un cúmulo de operaciones entre los valores originales de la matriz y los relacionados con las operaciones de fila en el proceso de reducción.

Ahora bien, aquí se produce un sistema de ecuaciones de tres variables y dos ecuaciones; en donde la tercer variable quedará libre; ésta última variable podrá adoptar cualquier número real y será esta una vez que se le haya asignado un valor la que hará posible la solución de un sistema 2X2 y dado que esta tercer variable puede adoptar infinidad de valores en el campo de los números reales, así mismo, el conjunto solución podrá adoptar infinidad de valores y combinaciones correspondientes al sistema 2X2 formado cuando se le asigna un valor a la tercer variable, lo cual hará posible la generación en R2 en este caso. Y en un caso general en donde la matriz tiene una dimensión mxn, con m<n y una configuración como la presentada en este caso, se presentará la generación en Rm. El sistema formado se muestra a continuación:

Sistema representado con variables. (Caso I)

Restando el término de la variable libre en ambos lados de la igualdad de las ecuaciones se tiene:

 Sustituyendo la variable x2 en la primer ecuación se tiene:

Despejando x1:

Como x3 es libre, quiere decir que puede adoptar cualquier valor real; esto nos indica que se puede generar un abanico infinito de soluciones en el sistema; al final, x1 y x2, serán constantes y se formará un vector solución (x1,x2,x3) distinto a cada valor de x3. Sin embargo, aquí lo que nos interesa es responder la siguiente pregunta: ¿Pueden las columnas de esta matriz generar R2?

Si las columnas de la matriz generan R2, entonces las componentes b1 y b2, podrán tomar cualquier valor real formándose así infinitas combinaciones de vectores (b1,b2), por tanto, la pregunta que nos revelará si las columnas de la matriz generan R2 será: ¿Pueden las componentes b1 y b2 tomar cualquier valor real? 

La respuesta corta es sí. A continuación se describe la justificación:

Como ya habíamos dictaminado; la variable x3 del sistema es libre; por lo cual si:

Entonces siempre existirá una solución del sistema ya que los únicos casos en los que se encontraría una inconsistencia sería que al dar un valor cualquiera a b1 y b2, se realizara la división entre cero o se determinara una raíz cuadrada de un número real negativo en las operaciones de reducción por filas, sin embargo; éstas operaciones (dividir entre cero y determinar la raíz cuadrada de un número) son operaciones que no se realizan en las operaciones de reducción por filas. Por ello, tanto b1 como b2, podrán adoptar cualquier valor real y el sistema presentará una consistencia. 

Caso II:

Matriz consistente condicionada.

 

El otro caso de consistencia se presentará siempre que *b2=0, más sin embargo; aquí ya hablamos de cierta condición o limitación en los valores que pueda adoptar (b1,b2) para que después de realizar el proceso de reducción por filas la entrada correspondiente al lugar de *b2 sea igual a cero. Por tanto, hablamos de ciertos valores que (b1,b2) puedan adoptar para que el sistema sea consistente.

Conclusión: Las columnas de una matriz que después de realizar el procedimiento de reducción por filas se llega a esta configuración no puede generar R2.

Convertidor de unidades.

Convierte las unidades deseadas rápidamente con este programa, genera nuevas unidades de medida o añade muevas unidades de medida.

Las unidades de medida con las que cuenta este convertidor son:

• Masa:
  Slug
  Kg
• Tiempo:
  Segundo
  Minuto
  Hora
  Día
• Longitud:
  in
  ft
  m
  km
  mi
  yd (yarda)
  
• Fuerza:
  Lb
  N
  Oz (onza)
  Kg
• Ángulo:
  rad (radianes)
  Grados
  Rev (Revoluciones)
  
• Área:
  mm2
  cm2
  m2
  in2
  ft2
  acre
  hectárea
• Potencia:
  Hp (Caballos fuerza)
  Kw (Kilowatts)
  lbft/s
• Presión:
  lb/in2
  Pa (Pascales)
  
• Volumen:
  Gl (galón)
  L
  Barril
  mm3
  cm3
  m3
  in3
  ft3
  in3

Los datos para adquirirlo así como el funcionamiento del mismo, se encuentran el siguiente video:

¿Pueden las columnas de una matriz de dimensión mxn generar Rm si m>n?

Sea una matriz A de dimensión 3X2 de componentes:

Matriz 3x2 general.

 

Entonces deseamos saber si cualquier vector en R3 puede ser generado por la combinación lineal de las columnas de A. Por lo que al construir nuestra matriz aumentada se tendrá:

Matriz aumentada.

 El siguiente paso consistirá en construir la matriz reducida, en donde se podrán dar solo dos opciones. Las cuales son: O la matriz es consistente o la matriz es inconsistente. Sabemos que una matriz inconsistente no puede generar Rm, por el contrario, una matriz consistente sí lo puede pero no cuando m>n, por la siguiente razón: 

Una matriz con esta característica no podrá generar R3, debido a que los valores de la columna aumentada (b1,b2,b3) estarán condicionados a adoptar ciertos valores para que la matriz sea consistente. Lo dicho anteriormente, se muestra a continuación:

1. 

   Matriz reducida.

    En donde el símbolo "*" denota el nuevo valor de la entrada de la matriz después de realizar las operaciones de reducción por filas. 

   Si la matriz es consistente; entonces *b3=0 y poseerá una ecuación de la siguiente forma:

   

   Ecuación 1.

    
   

    

   Como se mencionó anteriormente, los valores de b1,b2 y b3, estarán condicionados a adoptar valores tales que hagan que la ecuación se satisfaga, situación particular que imposibilita que A pueda generar R3.

   Conclusión: Una matriz de dimensión mxn con m>n NO puede generar Rm.
   

A continuación, se muestra un ejercicio en donde se muestran las operaciones que en esta entrada se denotan con el símbolo "*".

Imagen: Explicación del por qué una matriz con más filas que columnas no puede generar Rm.

Función real de varias variables independientes.

 Una función real con varias variables independientes, será aquella función que tiene más de dos variables, de las cuales una sola variable depende de los valores reales que adopten las variables independientes; puede tener "n" variables independientes, pero solamente una variable dependiente.

Al ser una función de más de dos variables su gráfica habitará en Rn con n>2 (*) y tendrá una regla de correspondencia de la siguiente forma:

Regla de correspondencia de función real con varias variables independientes.

En donde: 

Es el dominio de W.

 Y "n" será el número de variables independientes de la función. Éstas variables, podrán adoptar cualquier valor real, modificando el valor de la variable dependiente W. 

Debido a que se trata de una función, para cada valor de sus variables independientes, existirá un único valor de W (o de la variable dependiente) que no volverá a repetirse ante la variación de cualquier variable independiente. 

Para que se comprenda mejor esta situación, tome en cuenta la siguiente regla de correspondencia:

Regla de correspondencia de una función en R3.

 

En esta regla de correspondencia, las variables independientes son "x" y "y"; y la dependiente es "z" que está expresada en términos de "x" y "y". Si es una función en R3, para cada valor real que adopte "x" y "y", existirá un único valor de "z" que no volverá a repetirse ante la variación de los valores de "x" y "y".

En R2, podía trazarse una línea vertical paralela al eje "y" de tal forma que se origine una intersección entre la curva y la línea paralela al eje "y". Si la curva era una función, entonces dicha recta vertical solamente tendría un punto de intersección. Si la curva tiene más de un solo punto de intersección; entonces no es una función.

Lo mismo pasará en R3. Si trazamos sobre la superficie una línea vertical paralela al eje "z" de tal forma que se intercepte con la gráfica de la función, tendremos como resultado un solo punto de intersección. Si llegase a existir más de un solo punto de intersección, entonces podremos estar seguros que dicha gráfica no es una función en R3.

A continuación se muestra una gráfica de una función de tres variables.

Gráfica de una función de tres variables en R3.

La gráfica mostrada anteriormente tiene la ecuación: z=sen(xy) y las cuatro imágenes muestran la gráfica de la misma ecuación con distinta rotación e inclinación para que el lector pueda apreciar de mejor forma la gráfica. En teoría, si trazamos una línea vertical, paralela al eje "z" en cualquier punto de la gráfica, solamente se tocará un solo punto de intersección entre la línea y la gráfica.

Notas:

(*) Sin embargo, como no es posible graficar más de 3 ejes perpendiculares entre sí, podremos visualizar únicamente gráficas de funciones reales con hasta dos variables independientes y una dependiente.

Bibliografía:

Arcos Quezada, José Ismael. Cálculo para estudiantes de ingeniería 2. Editorial Kali. Toluca, México. (2022). Pág: 3-9.

Concavidad de una curva.

Existen dos tipos de concavidades para analizar y visualizar la curvatura de una ecuación en R2, las cuales se mencionan a continuación:

1) Concavidad hacia arriba.

Sea una función y=f(x) con "x" como variable independiente cuyo dominio pertenece a los reales de tal forma que es posible seccionar su dominio en dos partes cuya característica hace que una parte del dominio describa una curva "decreciente" (1) y en la otra parte de su dominio se tendrá una curva "creciente" (2). La siguiente imagen muestra una concavidad hacia arriba:

Gráfica 1: Concavidad hacia arriba.

La siguiente imagen muestra los intervalos del dominio de la variable independiente en los que la gráfica es decreciente y creciente, según lo mencionado anteriormente.

Gráfica 2: Intervalos decreciente y creciente de la gráfica 1.

Como se puede observar, es posible partir una gráfica de una curva en dos partes (no necesariamente tienen que ser simétricas) en donde termina el recorrido de una curva decreciente y comienza el recorrido de una curva creciente. 

2) Concavidad hacia abajo.

En este caso, la curva que representa este caso, posee las condiciones inversas a la curva presentada en el caso anterior. Esto es:

1. Comienza con un intervalo creciente.
2. En un punto de la curva se hace el cambio de dirección hacia un intervalo decreciente.

Lo dicho anteriormente, se muestra en las siguientes imágenes:

Gráfica 3: concavidad hacia abajo.

Los tramos creciente y decreciente de la gráfica quedarán ubicados como se muestra en la siguiente imagen:

Gráfica 4: Intervalos creciente y decreciente de la gráfica 3.

En R2 no existe otro tipo concavidad distinta a las mostradas en esta entrada.

En resumen, para distinguir el tipo de concavidad de una curva basta con visualizar la curvatura de la curva e identificar conforme al recorrido del dominio de la gráfica el intervalo creciente/decreciente y el punto en que se hace un cambio de intervalo a decreciente/creciente según corresponda el tipo de concavidad de la curva.

Notas.

(1) Es decir que mientras la variable "x" aumenta de valor f(x) disminuye su valor.

(2) Esto es: mientras la variable "x" aumenta de valor también lo hace f(x).

Bibliografía.

Arcos Quezada, Ismael. Cálculo infinitesimal para estudiantes de ingeniería, 3a. Edición. Editorial Kali-Xotl. Toluca, México. 2011. Pp. 92-95.