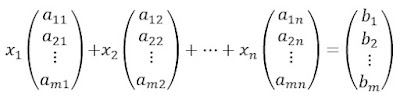En esta publicación se procederá a explicar el siguiente teorema del Álgebra Lineal:
TEOREMA 4:
Sea A una matriz de mxn. Entonces, las siguientes afirmaciones son lógicamente equivalentes. Esto es, para una A en particular, todas estas afirmaciones son verdaderas o falsas.
- Para cada b en Rm, la ecuación Ax=b tiene una solución.
- Cada b en Rm es una combinación lineal de las columnas de A.
- Las columnas de A generan Rm.
- A tiene una posición pivote en cada fila.(1)
Al formular la explicación, inherentemente también se estará formulando la demostración del teorema.
Como puede apreciarse, en la demostración de este teorema se involucran los siguientes temas del Álgebra Lineal y por ende, se recomienda que el lector los estudie para tener una mejor comprensión de esta publicación:
- Ecuación matricial Ax=b.
- Combinaciones lineales.
- Generación de vectores en Rm.
- Posición pivote de una matriz.
Empezaremos definiendo nuestra matriz A y nuestro vector b.
Sea:
Entonces la ecuación matricial Ax=b, quedará expresada como:
En donde las entradas de la matriz A (2) son constantes numéricas pertenecientes al conjunto numérico de los reales; las entradas del vector x (3) son variables incógnitas tales que al realizar la multiplicación con la matriz A, nos arrojará el vector b.
Ahora bien; para descubrir los "n" valores del vector "x", tales que multiplicados por la matriz A, nos arroje el vector "b", será necesario construir una matriz aumentada (4) y hacer la correspondiente reducción por filas, dejando una posición pivote (5) sobre la diagonal principal (6) de la matriz y posteriormente realizar la correspondiente reducción por filas (7) para descubrir el valor de cada incógnita del vector "x".
A continuación se muestra el proceso descrito en el párrafo anterior:
- Construyendo la matriz aumentada:
- Generando la matriz reducida:
Al tomar para desarrollo de esta publicación una matriz de dimensión mxn, no se realizarán estrictamente las operaciones de reducción como se realizarían con una matriz de dimensiones conocidas por números reales. En su caso se colocará un * en la simbología de las entradas que indicará el valor nuevo de la entrada con el subíndice indicado después de haber realizado las operaciones de reducción de fila.
Aquí se podrán presentar los siguientes casos:
La estructura de la matriz resultante después de realizar el procedimiento de reducción puede ser la siguiente:
En donde la entrada corresponde a la posición "m" poseerá una combinación de operaciones (suma y resta), entre las distintas entradas anteriores del vector b, resultado de realizar el procedimiento de reducción. Esto se muestra a continuación para su mejor compresión:
En donde:
Y son los números resultantes de las operaciones de reducción que multiplican a los elementos de la columna aumentada. Observe que el elemento bm, no está multiplicando a una constante Cm, esto es debido a que la última fila no es afectada por la multiplicación directa de una constante con el objetivo de hacer "ceros" en las entradas que se encuentran por debajo de la posición pivote de la matriz.
Ahora bien, la matriz será consistente siempre que *bm=0.
Es decir, si:
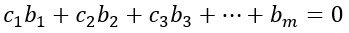 |
Ecuación 1.
|
Esto indicaría que el lugar correspondiente a la entrada *bm sería igual a cero, generando así, una consistencia en el sistema resultante, con la condición de que el vector b, solo y únicamente pueda adoptar los valores específicos y tales que al sustituirlos en la ecuación 1, se cumpla la igualdad.
Ahora bien, si analizamos esta situación y la comparamos con lo que dicta el teorema 4, llegaremos las siguientes conclusiones:
- No toda b en Rm, tiene una solución para la ecuación matricial Ax=b.
Esto es debido a que en todo el universo de vectores que puedan existir en Rm, existe una colección de vectores, tales que al sustituir los valores de sus entradas en la ecuación 1, se producirá una desigualdad, generando así un sistema inconsistente (8). - No toda b en Rm es una combinación lineal de las columnas de la matriz A.
Esto es debido a que existe una colección de valores de b, tales que se produce una inconsistencia en el sistema. - Las columnas de A no generan Rm.
Si todas las columnas de A generaran Rm, entonces el sistema sería consistente sin tener ninguna restricción; como no todas las colecciones de vectores contenidos en Rm cumplen la condición de satisfacer la ecuación 1, las columnas de A, no podrán generar Rm. - A no tiene una posición pivote en cada fila de A.
Como puede observarse, todos los enunciados del teorema 4 son falsos en una matriz que posee esta estructura. En caso de que la matriz no sea consistente, es decir que toque la posibilidad de que no se cumpla la igualdad de la ecuación 1, entonces cotejando con los enunciados del teorema 4, descubriremos que igualmente los 4 enunciados serán falsos.
Cabe aclarar que cuando se produce un sistema inconsistente, entonces se estará formando una ecuación del tipo:
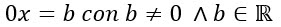 |
Ecuación 2: Inconsistencia.
|
Y en la respuesta que genera la siguiente pregunta es cuando se puede vislumbrar la inconsistencia que yace en la ecuación 2. La siguiente pregunta se formula a partir de lo que la ecuación 2, es capaz de decirnos y revelarnos. ¿Qué número real es capaz de ser multiplicado por el número cero y darnos como resultado el número real b que no es cero? Dado que todo número real que es multiplicado por cero da como resultado cero, entonces podremos decir que en el campo de los números reales no existe valor real que sea capaz de satisfacer esta igualdad; por tanto en el conjunto de los números reales se declarará el sistema como inconsistente a aquél que posee una ecuación de este tipo.
El otro caso que puede producirse es el contrario al mostrado en el inciso anterior, es decir; que la matriz A tenga una posición pivote en cada fila. Como se muestra a continuación:
Observe que una matriz aumentada con esta estructura no está condicionada a que la ecuación 1 deba ser igual a cero, en este caso, la entrada correspondiente al lugar bm puede adoptar cualquier valor real sin estar sujeto a alguna restricción. Este hecho; nos conlleva a afirmar la veracidad de los cuatro enunciados del teorema 4 que a continuación se analizan uno por uno teniendo esta situación.
- Para cada b en Rm, la ecuación Ax=b tiene una solución.
Debido a que la matriz aumentada posee una posición pivote en cada fila de la matriz A, es posible que el vector b pueda adoptar cualquier valor en Rm y ser consistente con la ecuación matricial Ax=b. - Cada b en Rm es una combinación lineal de las columnas de A.
Sean los pesos:
Tales que al multiplicarlos respectivamente por cada una de las columnas de A, nos dará como resultado un vector b en Rm. Esto es:
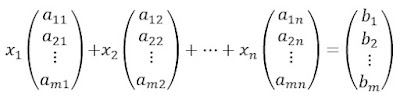 |
Ecuación 3: combinación lineal de las columnas de A.
|
Ahora bien, la ecuación 3 puede expresarse como una ecuación matricial Ax=b. (9)
Una vez que obtenemos esta visualización de la ecuación 3, es posible organizar la matriz aumentada para así realizar el procedimiento de reducción por filas y determinar los valores de los pesos de "x". Ahora bien, si en el punto uno, ya se determinó que la matriz es consistente y tiene una posición pivote en cada fila de A, entonces al realizar el proceso de reducción por filas y formar nuestro sistema de ecuaciones llegaremos a la misma conclusión que el punto 1, el sistema será consistente y habrá una posición pivote en cada una de las filas de A, generando así un abanico infinito de combinaciones posibles que pueden ser soluciones del mismo sistema.
3. Las columnas de A generan Rm.
Como ya vimos en los puntos anteriores, existe una infinidad de combinaciones lineales que pueden ser soluciones del sistema y que dichas combinaciones se encuentran todas y sin restricción alguna en Rm, lo cual nos conlleva a decir que las columnas de A, pueden generar cualquier vector contenido en Rm.
4. A tiene una posición pivote en cada fila.
Como puede observarse, para que se den todas las condiciones anteriores, es necesario que la matriz tenga una posición pivote en cada fila de A.
Preguntas y respuestas.
1. ¿Pueden las columnas de una matriz de dimensión mxn generar Rm si m>n?
2. ¿Pueden las columnas de una matriz no cuadrada generar Rm?
Respuesta: depende de la dimensión de la matriz se tendrán los siguientes dos casos:
1.
Sea una matriz A de dimensión mxn con m>n, entonces esta matriz
posee la característica de tener más filas que columnas, por tanto la respuesta es no. Para consultar la justificación de esta respuesta hacer clic en el siguiente enlace: ¿Puede una matriz con más filas que columnas generar Rm?
2.
Sea una matriz A de dimensión mxn con m<n, entonces esta matriz
posee la característica de tener más columnas que filas, por tanto la respuesta es sí. La justificación se presenta a continuación en el siguiente enlace: ¿Puede una matriz con más columnas que filas generar Rm?
Notas y Referencias.
(1) C. Lay, David. Álgebra Lineal y sus Aplicaciones. Tercera edición, editorial PEARSON Addison Wesley, 2007, pág. 43.
(2) Se entenderá por matriz al arreglo ordenado de números reales dispuestos en renglones y columnas, en donde cada número que compone la matriz recibirá el nombre de "entrada" y se podrá ubicar por medio de dos subíndices que indicarán el número de fila y de columna donde se encuentra ubicado el número en la matriz.
(3) Se entenderá por vector al arreglo ordenado con "m" o "n" número de filas y una sola columna; en donde "m" y "n" serán números reales y además; dicho vector posee magnitud, dirección y sentido. El vector también podrá visualizarse con "m" o "n" número de columnas y una sola fila.
(4) De una ecuación matricial Ax=b, se entiende por matriz aumentada a aquella matriz que está multiplicando al vector incógnita y que se le ha aumentado una columna cuyos valores corresponden al vector b.
(5) Una posición pivote corresponde a una entrada ubicada sobre la diagonal principal de la matriz que puede tener subíndices 11, 22, 33, 44, etc. Cuyo valor de la entrada será igual a la unidad.
(6) Se entenderá por diagonal principal a todas las entradas de una matriz de dimensión mxn (con m y n pertenecientes a los reales y distintos de 0 y 1), cuyos valores de subíndices son iguales.
(7) El proceso de reducción por filas consiste en generar posiciones pivote en la diagonal principal de la matriz y por debajo de esa posición pivote, generar entradas con valor igual a cero, para ello es necesario realizar las correspondientes operaciones de multiplicación, división, suma o resta, entre las distintas filas de la matriz.
(8) Se dice que una matriz es inconsistente, cuando el sistema no tiene solución; esto se cumple cuando una entrada que "debería" ser posición pivote para que exista una solución es cero y en la columna aumentada existe un valor distinto de cero.
(9) Haga de cuenta que si realizamos el producto fila-columna de la ecuación matricial, es posible descomponer la visualización de la ecuación en forma matricial al de la ecuación 3 que usualmente suele denominarse con el nombre de "ecuación vectorial".