Concavidad de una curva.

Existen dos tipos de concavidades para analizar y visualizar la curvatura de una ecuación en R2, las cuales se mencionan a continuación:

1) Concavidad hacia arriba.

Sea una función y=f(x) con "x" como variable independiente cuyo dominio pertenece a los reales de tal forma que es posible seccionar su dominio en dos partes cuya característica hace que una parte del dominio describa una curva "decreciente" (1) y en la otra parte de su dominio se tendrá una curva "creciente" (2). La siguiente imagen muestra una concavidad hacia arriba:

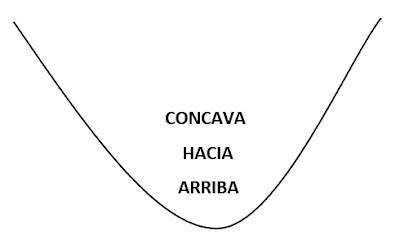Gráfica 1: Concavidad hacia arriba.

La siguiente imagen muestra los intervalos del dominio de la variable independiente en los que la gráfica es decreciente y creciente, según lo mencionado anteriormente.

Gráfica 2: Intervalos decreciente y creciente de la gráfica 1.

Como se puede observar, es posible partir una gráfica de una curva en dos partes (no necesariamente tienen que ser simétricas) en donde termina el recorrido de una curva decreciente y comienza el recorrido de una curva creciente. 

2) Concavidad hacia abajo.

En este caso, la curva que representa este caso, posee las condiciones inversas a la curva presentada en el caso anterior. Esto es:

1. Comienza con un intervalo creciente.
2. En un punto de la curva se hace el cambio de dirección hacia un intervalo decreciente.

Lo dicho anteriormente, se muestra en las siguientes imágenes:

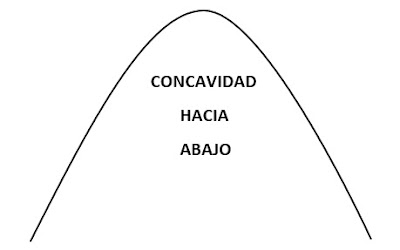Gráfica 3: concavidad hacia abajo.

Los tramos creciente y decreciente de la gráfica quedarán ubicados como se muestra en la siguiente imagen:

Gráfica 4: Intervalos creciente y decreciente de la gráfica 3.

En R2 no existe otro tipo concavidad distinta a las mostradas en esta entrada.

En resumen, para distinguir el tipo de concavidad de una curva basta con visualizar la curvatura de la curva e identificar conforme al recorrido del dominio de la gráfica el intervalo creciente/decreciente y el punto en que se hace un cambio de intervalo a decreciente/creciente según corresponda el tipo de concavidad de la curva.

Notas.

(1) Es decir que mientras la variable "x" aumenta de valor f(x) disminuye su valor.

(2) Esto es: mientras la variable "x" aumenta de valor también lo hace f(x).

Bibliografía.

Arcos Quezada, Ismael. Cálculo infinitesimal para estudiantes de ingeniería, 3a. Edición. Editorial Kali-Xotl. Toluca, México. 2011. Pp. 92-95.