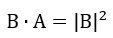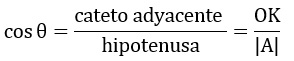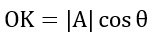¿Puede una matriz con más columnas que filas generar Rm?

Respuesta: Sea una matriz A de dimensión mxn con m<n, entonces esta matriz posee la característica de tener más columnas que filas, por tanto la respuesta es sí. La justificación se presenta a continuación:

Téngase en consideración una matriz A de dimensión 2x3 cuya configuración general se muestra a continuación:

Matriz general 2x3.

 

Por tanto, la matriz aumentada quedará representada como:

Matriz general 2x3 aumentada.

 Como el vector que se aumentó a la matriz A tiene dos componentes (b1 y b2), querrá decir que se procederá a evaluar si las columnas de A pueden generar R2, para ello será necesario determinar la matriz reducida de A aumentada.

Siempre y cuando la matriz presente una consistencia, podrán producirse los siguientes dos casos:

Caso I:

Matriz aumentada general en caso I.

Recordemos que el símbolo (*) significa que dicha entrada tiene un cúmulo de operaciones entre los valores originales de la matriz y los relacionados con las operaciones de fila en el proceso de reducción.

Ahora bien, aquí se produce un sistema de ecuaciones de tres variables y dos ecuaciones; en donde la tercer variable quedará libre; ésta última variable podrá adoptar cualquier número real y será esta una vez que se le haya asignado un valor la que hará posible la solución de un sistema 2X2 y dado que esta tercer variable puede adoptar infinidad de valores en el campo de los números reales, así mismo, el conjunto solución podrá adoptar infinidad de valores y combinaciones correspondientes al sistema 2X2 formado cuando se le asigna un valor a la tercer variable, lo cual hará posible la generación en R2 en este caso. Y en un caso general en donde la matriz tiene una dimensión mxn, con m<n y una configuración como la presentada en este caso, se presentará la generación en Rm. El sistema formado se muestra a continuación:

Sistema representado con variables. (Caso I)

Restando el término de la variable libre en ambos lados de la igualdad de las ecuaciones se tiene:

 Sustituyendo la variable x2 en la primer ecuación se tiene:

Despejando x1:

Como x3 es libre, quiere decir que puede adoptar cualquier valor real; esto nos indica que se puede generar un abanico infinito de soluciones en el sistema; al final, x1 y x2, serán constantes y se formará un vector solución (x1,x2,x3) distinto a cada valor de x3. Sin embargo, aquí lo que nos interesa es responder la siguiente pregunta: ¿Pueden las columnas de esta matriz generar R2?

Si las columnas de la matriz generan R2, entonces las componentes b1 y b2, podrán tomar cualquier valor real formándose así infinitas combinaciones de vectores (b1,b2), por tanto, la pregunta que nos revelará si las columnas de la matriz generan R2 será: ¿Pueden las componentes b1 y b2 tomar cualquier valor real? 

La respuesta corta es sí. A continuación se describe la justificación:

Como ya habíamos dictaminado; la variable x3 del sistema es libre; por lo cual si:

Entonces siempre existirá una solución del sistema ya que los únicos casos en los que se encontraría una inconsistencia sería que al dar un valor cualquiera a b1 y b2, se realizara la división entre cero o se determinara una raíz cuadrada de un número real negativo en las operaciones de reducción por filas, sin embargo; éstas operaciones (dividir entre cero y determinar la raíz cuadrada de un número) son operaciones que no se realizan en las operaciones de reducción por filas. Por ello, tanto b1 como b2, podrán adoptar cualquier valor real y el sistema presentará una consistencia. 

Caso II:

Matriz consistente condicionada.

 

El otro caso de consistencia se presentará siempre que *b2=0, más sin embargo; aquí ya hablamos de cierta condición o limitación en los valores que pueda adoptar (b1,b2) para que después de realizar el proceso de reducción por filas la entrada correspondiente al lugar de *b2 sea igual a cero. Por tanto, hablamos de ciertos valores que (b1,b2) puedan adoptar para que el sistema sea consistente.

Conclusión: Las columnas de una matriz que después de realizar el procedimiento de reducción por filas se llega a esta configuración no puede generar R2.

Convertidor de unidades.

Convierte las unidades deseadas rápidamente con este programa, genera nuevas unidades de medida o añade muevas unidades de medida.

Las unidades de medida con las que cuenta este convertidor son:

• Masa:
  Slug
  Kg
• Tiempo:
  Segundo
  Minuto
  Hora
  Día
• Longitud:
  in
  ft
  m
  km
  mi
  yd (yarda)
  
• Fuerza:
  Lb
  N
  Oz (onza)
  Kg
• Ángulo:
  rad (radianes)
  Grados
  Rev (Revoluciones)
  
• Área:
  mm2
  cm2
  m2
  in2
  ft2
  acre
  hectárea
• Potencia:
  Hp (Caballos fuerza)
  Kw (Kilowatts)
  lbft/s
• Presión:
  lb/in2
  Pa (Pascales)
  
• Volumen:
  Gl (galón)
  L
  Barril
  mm3
  cm3
  m3
  in3
  ft3
  in3

Los datos para adquirirlo así como el funcionamiento del mismo, se encuentran el siguiente video:

¿Pueden las columnas de una matriz de dimensión mxn generar Rm si m>n?

Sea una matriz A de dimensión 3X2 de componentes:

Matriz 3x2 general.

 

Entonces deseamos saber si cualquier vector en R3 puede ser generado por la combinación lineal de las columnas de A. Por lo que al construir nuestra matriz aumentada se tendrá:

Matriz aumentada.

 El siguiente paso consistirá en construir la matriz reducida, en donde se podrán dar solo dos opciones. Las cuales son: O la matriz es consistente o la matriz es inconsistente. Sabemos que una matriz inconsistente no puede generar Rm, por el contrario, una matriz consistente sí lo puede pero no cuando m>n, por la siguiente razón: 

Una matriz con esta característica no podrá generar R3, debido a que los valores de la columna aumentada (b1,b2,b3) estarán condicionados a adoptar ciertos valores para que la matriz sea consistente. Lo dicho anteriormente, se muestra a continuación:

1. 

   Matriz reducida.

    En donde el símbolo "*" denota el nuevo valor de la entrada de la matriz después de realizar las operaciones de reducción por filas. 

   Si la matriz es consistente; entonces *b3=0 y poseerá una ecuación de la siguiente forma:

   

   Ecuación 1.

    
   

    

   Como se mencionó anteriormente, los valores de b1,b2 y b3, estarán condicionados a adoptar valores tales que hagan que la ecuación se satisfaga, situación particular que imposibilita que A pueda generar R3.

   Conclusión: Una matriz de dimensión mxn con m>n NO puede generar Rm.
   

A continuación, se muestra un ejercicio en donde se muestran las operaciones que en esta entrada se denotan con el símbolo "*".

Imagen: Explicación del por qué una matriz con más filas que columnas no puede generar Rm.

Función real de varias variables independientes.

 Una función real con varias variables independientes, será aquella función que tiene más de dos variables, de las cuales una sola variable depende de los valores reales que adopten las variables independientes; puede tener "n" variables independientes, pero solamente una variable dependiente.

Al ser una función de más de dos variables su gráfica habitará en Rn con n>2 (*) y tendrá una regla de correspondencia de la siguiente forma:

Regla de correspondencia de función real con varias variables independientes.

En donde: 

Es el dominio de W.

 Y "n" será el número de variables independientes de la función. Éstas variables, podrán adoptar cualquier valor real, modificando el valor de la variable dependiente W. 

Debido a que se trata de una función, para cada valor de sus variables independientes, existirá un único valor de W (o de la variable dependiente) que no volverá a repetirse ante la variación de cualquier variable independiente. 

Para que se comprenda mejor esta situación, tome en cuenta la siguiente regla de correspondencia:

Regla de correspondencia de una función en R3.

 

En esta regla de correspondencia, las variables independientes son "x" y "y"; y la dependiente es "z" que está expresada en términos de "x" y "y". Si es una función en R3, para cada valor real que adopte "x" y "y", existirá un único valor de "z" que no volverá a repetirse ante la variación de los valores de "x" y "y".

En R2, podía trazarse una línea vertical paralela al eje "y" de tal forma que se origine una intersección entre la curva y la línea paralela al eje "y". Si la curva era una función, entonces dicha recta vertical solamente tendría un punto de intersección. Si la curva tiene más de un solo punto de intersección; entonces no es una función.

Lo mismo pasará en R3. Si trazamos sobre la superficie una línea vertical paralela al eje "z" de tal forma que se intercepte con la gráfica de la función, tendremos como resultado un solo punto de intersección. Si llegase a existir más de un solo punto de intersección, entonces podremos estar seguros que dicha gráfica no es una función en R3.

A continuación se muestra una gráfica de una función de tres variables.

Gráfica de una función de tres variables en R3.

La gráfica mostrada anteriormente tiene la ecuación: z=sen(xy) y las cuatro imágenes muestran la gráfica de la misma ecuación con distinta rotación e inclinación para que el lector pueda apreciar de mejor forma la gráfica. En teoría, si trazamos una línea vertical, paralela al eje "z" en cualquier punto de la gráfica, solamente se tocará un solo punto de intersección entre la línea y la gráfica.

Notas:

(*) Sin embargo, como no es posible graficar más de 3 ejes perpendiculares entre sí, podremos visualizar únicamente gráficas de funciones reales con hasta dos variables independientes y una dependiente.

Bibliografía:

Arcos Quezada, José Ismael. Cálculo para estudiantes de ingeniería 2. Editorial Kali. Toluca, México. (2022). Pág: 3-9.

Concavidad de una curva.

Existen dos tipos de concavidades para analizar y visualizar la curvatura de una ecuación en R2, las cuales se mencionan a continuación:

1) Concavidad hacia arriba.

Sea una función y=f(x) con "x" como variable independiente cuyo dominio pertenece a los reales de tal forma que es posible seccionar su dominio en dos partes cuya característica hace que una parte del dominio describa una curva "decreciente" (1) y en la otra parte de su dominio se tendrá una curva "creciente" (2). La siguiente imagen muestra una concavidad hacia arriba:

Gráfica 1: Concavidad hacia arriba.

La siguiente imagen muestra los intervalos del dominio de la variable independiente en los que la gráfica es decreciente y creciente, según lo mencionado anteriormente.

Gráfica 2: Intervalos decreciente y creciente de la gráfica 1.

Como se puede observar, es posible partir una gráfica de una curva en dos partes (no necesariamente tienen que ser simétricas) en donde termina el recorrido de una curva decreciente y comienza el recorrido de una curva creciente. 

2) Concavidad hacia abajo.

En este caso, la curva que representa este caso, posee las condiciones inversas a la curva presentada en el caso anterior. Esto es:

1. Comienza con un intervalo creciente.
2. En un punto de la curva se hace el cambio de dirección hacia un intervalo decreciente.

Lo dicho anteriormente, se muestra en las siguientes imágenes:

Gráfica 3: concavidad hacia abajo.

Los tramos creciente y decreciente de la gráfica quedarán ubicados como se muestra en la siguiente imagen:

Gráfica 4: Intervalos creciente y decreciente de la gráfica 3.

En R2 no existe otro tipo concavidad distinta a las mostradas en esta entrada.

En resumen, para distinguir el tipo de concavidad de una curva basta con visualizar la curvatura de la curva e identificar conforme al recorrido del dominio de la gráfica el intervalo creciente/decreciente y el punto en que se hace un cambio de intervalo a decreciente/creciente según corresponda el tipo de concavidad de la curva.

Notas.

(1) Es decir que mientras la variable "x" aumenta de valor f(x) disminuye su valor.

(2) Esto es: mientras la variable "x" aumenta de valor también lo hace f(x).

Bibliografía.

Arcos Quezada, Ismael. Cálculo infinitesimal para estudiantes de ingeniería, 3a. Edición. Editorial Kali-Xotl. Toluca, México. 2011. Pp. 92-95.

Generación de vectores en un espacio de dimensión "m".

 En esta publicación se procederá a explicar el siguiente teorema del Álgebra Lineal:

TEOREMA 4: 

Sea A una matriz de mxn. Entonces, las siguientes afirmaciones son lógicamente equivalentes. Esto es, para una A en particular, todas estas afirmaciones son verdaderas o falsas.

1. Para cada b en Rm, la ecuación Ax=b tiene una solución.
2. Cada b en Rm es una combinación lineal de las columnas de A.
3. Las columnas de A generan Rm.
4. A tiene una posición pivote en cada fila.(1)

 Al formular la explicación, inherentemente también se estará formulando la demostración del teorema.  

Como puede apreciarse, en la demostración de este teorema se involucran los siguientes temas del Álgebra Lineal y por ende, se recomienda que el lector los estudie para tener una mejor comprensión de esta publicación:

1. Ecuación matricial Ax=b.
2. Combinaciones lineales.
3. Generación de vectores en Rm.
4. Posición pivote de una matriz.

Empezaremos definiendo nuestra matriz A y nuestro vector b.

Sea: 

 Entonces la ecuación matricial Ax=b, quedará expresada como:

En donde las entradas de la matriz  A (2) son constantes numéricas pertenecientes al conjunto numérico de los reales; las entradas del vector  x  (3) son variables incógnitas tales que al realizar la multiplicación con la matriz A, nos arrojará el vector b.

Ahora bien; para descubrir los "n" valores del vector "x", tales que multiplicados por la matriz A, nos arroje el vector "b", será necesario construir una matriz aumentada (4) y hacer la correspondiente reducción por filas, dejando una posición pivote (5) sobre la diagonal principal (6) de la matriz y posteriormente realizar la correspondiente reducción por filas (7) para descubrir el valor de cada incógnita del vector "x". 

A continuación se muestra el proceso descrito en el párrafo anterior:

• Construyendo la matriz aumentada:

• Generando la matriz reducida:

Al tomar para desarrollo de esta publicación una matriz de dimensión mxn, no se realizarán estrictamente las operaciones de reducción como se realizarían con una matriz de dimensiones conocidas por números reales. En su caso se colocará un * en la simbología de las entradas que indicará el valor nuevo de la entrada con el subíndice indicado después de haber realizado las operaciones de reducción de fila.

Aquí se podrán presentar los siguientes casos: 

• Una matriz condicionada.

La estructura de la matriz resultante después de realizar el procedimiento de reducción puede ser la siguiente:

En donde la entrada corresponde a la posición "m" poseerá una combinación de operaciones (suma y resta), entre las distintas entradas anteriores del vector b, resultado de realizar el procedimiento de reducción. Esto se muestra a continuación para su mejor compresión:

  En donde:

Y son los números resultantes de las operaciones de reducción que multiplican a los elementos de la columna aumentada. Observe que el elemento bm, no está multiplicando a una constante Cm, esto es debido a que la última fila no es afectada por la multiplicación directa de una constante con el objetivo de hacer "ceros" en las entradas que se encuentran por debajo de la posición pivote de la matriz.

Ahora bien, la matriz será consistente siempre que *bm=0.

Es decir, si:

Ecuación 1.

 

Esto indicaría que el lugar correspondiente a la entrada *bm sería igual a cero, generando así, una consistencia en el sistema resultante, con la condición de que el vector b, solo y únicamente pueda adoptar los valores específicos y tales que al sustituirlos en la ecuación 1, se cumpla la igualdad.

 

Ahora bien, si analizamos esta situación y la comparamos con lo que dicta el teorema 4, llegaremos las siguientes conclusiones:

1. No toda b en Rm, tiene una solución para la ecuación matricial Ax=b.
   Esto es debido a que en todo el universo de vectores que puedan existir en Rm, existe una colección de vectores, tales que al sustituir los valores de sus entradas en la ecuación 1, se producirá una desigualdad, generando así un sistema inconsistente (8).
2. No toda b en Rm es una combinación lineal de las columnas de la matriz A.
   Esto es debido a que existe una colección de valores de b, tales que se produce una inconsistencia en el sistema.
3. Las columnas de A no generan Rm.
    Si todas las columnas de A generaran Rm, entonces el sistema sería consistente sin tener ninguna restricción; como no todas las colecciones de vectores contenidos en Rm cumplen la condición de satisfacer la ecuación 1, las columnas de A, no podrán generar Rm.
4. A no tiene una posición pivote en cada fila de A.

Como puede observarse, todos los enunciados del teorema 4 son falsos en una matriz que posee esta estructura. En caso de que la matriz no sea consistente, es decir que toque la posibilidad de que no se cumpla la igualdad de la ecuación 1, entonces cotejando con los enunciados del teorema 4, descubriremos que igualmente los 4 enunciados serán falsos.

Cabe aclarar que cuando se produce un sistema inconsistente, entonces se estará formando una ecuación del tipo: 

Ecuación 2: Inconsistencia.

 

Y en la respuesta que genera la siguiente pregunta es cuando se puede vislumbrar la inconsistencia que yace en la ecuación 2. La siguiente pregunta se formula a partir de lo que la ecuación 2, es capaz de decirnos y revelarnos. ¿Qué número real es capaz de ser multiplicado por el número cero y darnos como resultado el número real b que no es cero? Dado que todo número real que es multiplicado por cero da como resultado cero, entonces podremos decir que en el campo de los números reales no existe valor real que sea capaz de satisfacer esta igualdad; por tanto en el conjunto de los números reales se declarará el sistema como inconsistente a aquél que posee una ecuación de este tipo.

• Una matriz consistente:
  

El otro caso que puede producirse es el contrario al mostrado en el inciso anterior, es decir; que la matriz A tenga una posición pivote en cada fila. Como se muestra a continuación:

Observe que una matriz aumentada con esta estructura no está condicionada a que la ecuación 1 deba ser igual a cero, en este caso, la entrada correspondiente al lugar bm puede adoptar cualquier valor real sin estar sujeto a alguna restricción. Este hecho; nos conlleva a afirmar la veracidad de los cuatro enunciados del teorema 4 que a continuación se analizan uno por uno teniendo esta situación.

1. Para cada b en Rm, la ecuación Ax=b tiene una solución.
   Debido a que la matriz aumentada posee una posición pivote en cada fila de la matriz A, es posible que el vector b pueda adoptar cualquier valor en Rm y ser consistente con la ecuación matricial Ax=b.
2. Cada b en Rm es una combinación lineal de las columnas de A.
   Sean los pesos:
   
   
   
   
   
   Tales que al multiplicarlos respectivamente por cada una de las columnas de A, nos dará como resultado un vector b en Rm. Esto es:
   
   

   

   Ecuación 3: combinación lineal de las columnas de A.
   

   
   Ahora bien, la ecuación 3 puede expresarse como una ecuación matricial Ax=b. (9)
   

Una vez que obtenemos esta visualización de la ecuación 3, es posible organizar la matriz aumentada para así realizar el procedimiento de reducción por filas y determinar los valores de los pesos de "x". Ahora bien, si en el punto uno, ya se determinó que la matriz es consistente y tiene una posición pivote en cada fila de A, entonces al realizar el proceso de reducción por filas y formar nuestro sistema de ecuaciones llegaremos a la misma conclusión que el punto 1, el sistema será consistente y habrá una posición pivote en cada una de las filas de A, generando así un abanico infinito de combinaciones posibles que pueden ser soluciones del mismo sistema.

3. Las columnas de A generan Rm.

 Como ya vimos en los puntos anteriores, existe una infinidad de combinaciones lineales que pueden ser soluciones del sistema y que dichas combinaciones se encuentran todas y sin restricción alguna en Rm, lo cual nos conlleva a decir que las columnas de A, pueden generar cualquier vector contenido en Rm.

4. A tiene una posición pivote en cada fila.

Como puede observarse, para que se den todas las condiciones anteriores, es necesario que la matriz tenga una posición pivote en cada fila de A.

Preguntas y respuestas.

1. ¿Pueden las columnas de una matriz de dimensión mxn generar Rm si m>n?

Respuesta: Haga clic aquí. 

    2. ¿Pueden las columnas de una matriz no cuadrada generar Rm?

Respuesta:  depende de la dimensión de la matriz se tendrán los siguientes dos casos:

1. Sea una matriz A de dimensión mxn con m>n, entonces esta matriz posee la característica de tener más filas que columnas, por tanto la respuesta es no. Para consultar la justificación de esta respuesta hacer clic en el siguiente enlace: ¿Puede una matriz con más filas que columnas generar Rm?

2. Sea una matriz A de dimensión mxn con m<n, entonces esta matriz posee la característica de tener más columnas que filas, por tanto la respuesta es sí. La justificación se presenta a continuación en el siguiente enlace: ¿Puede una matriz con más columnas que filas generar Rm?

Notas y Referencias. 

(1) C. Lay, David. Álgebra Lineal y sus Aplicaciones. Tercera edición, editorial PEARSON Addison Wesley, 2007, pág. 43. 

 (2) Se entenderá por matriz al arreglo ordenado de números reales dispuestos en renglones y columnas, en donde cada número que compone la matriz recibirá el nombre de "entrada" y se podrá ubicar por medio de dos subíndices que indicarán el número de fila y de columna donde se encuentra ubicado el número en la matriz.

(3) Se entenderá por vector al arreglo ordenado con "m" o "n" número de filas y una sola columna; en donde "m" y "n" serán números reales y además; dicho vector posee magnitud, dirección y sentido. El vector también podrá visualizarse con "m" o "n" número de columnas y una sola fila.

(4) De una ecuación matricial Ax=b, se entiende por matriz aumentada a aquella matriz que está multiplicando al vector incógnita y que se le ha aumentado una columna cuyos valores corresponden al vector b.

(5) Una posición pivote corresponde a una entrada ubicada sobre la diagonal principal de la matriz que puede tener subíndices 11, 22, 33, 44, etc. Cuyo valor de la entrada será igual a la unidad.

(6) Se entenderá por diagonal principal a todas las entradas de una matriz de dimensión mxn (con m y n pertenecientes a los reales y distintos de 0 y 1), cuyos valores de subíndices son iguales.

(7) El proceso de reducción por filas consiste en generar posiciones pivote en la diagonal principal de la matriz y por debajo de esa posición pivote, generar entradas con valor igual a cero, para ello es necesario realizar las correspondientes operaciones de multiplicación, división, suma o resta, entre las distintas filas de la matriz.

(8) Se dice que una matriz es inconsistente, cuando el sistema no tiene solución; esto se cumple cuando una entrada que "debería" ser posición pivote para que exista una solución es cero y en la columna aumentada existe un valor distinto de cero.

(9) Haga de cuenta que si realizamos el producto fila-columna de la ecuación matricial, es posible descomponer la visualización de la ecuación en forma matricial al de la ecuación 3 que usualmente suele denominarse con el nombre de "ecuación vectorial".

¿Cómo agregar comandos a la cinta de opciones de Excel?

   En ocasiones es necesario realizar tareas que involucran el activar comandos que no están a la vista en la cinta de opciones de Excel, ocasionando que la tarea se demore en tiempo por buscar el comando y realizar mayor cantidad de clics para poder acceder a él; en esta entrada se muestra el procedimiento para poder poner comandos que no es posible acceder a ellos con un solo clic en la cinta de opciones de Excel y que de esta forma sea posible acceder a ellos con un solo clic.

El producto punto.

El producto punto.

Autor: Alfredo Jiménez Colín.

 

En esta entrada se definirá el concepto del producto punto de dos vectores, también llamado "producto escalar".

El lector deberá tener los siguientes conocimientos para comprender las explicaciones que se darán en esta entrada:

1. Concepto de escalar.
2. Concepto de vector.
3. Razones trigonométricas.
4. Concepto de perpendicularidad.

Comenzaremos este escrito definiendo el producto punto o escalar, como Gordon Fuller lo define en su libro (1): 

Definición 10.6. El producto escalar de dos vectores A y B, que se designa por A°B, es el producto de sus longitudes multiplicado por el coseno del ángulo (teta) entre ellos. Esto es, 

La definición 10.6. se puede expresar gráficamente de la siguiente forma:

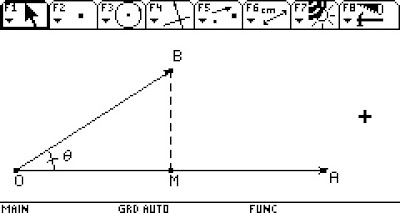Gráfica 1: Gráfica del producto punto.

En la imagen se puede apreciar que el vector A y el vector B, parten de un mismo punto O. Además, entre los dos vectores se forma un ángulo teta. Algo que vale la pena considerar es que el vector B es menor en tamaño que el vector A. 

Por lo tanto, se enunciará la siguiente definición:

    Definición 1: el producto punto A°B de dos vectores, será igual a la magnitud del vector A multiplicado por la proyección de B sobre A. 

¿Cuál es la proyección de B sobre A?

Imagine que en la parte superior de la imagen existe una lámpara que está iluminando la gráfica de arriba hacia abajo, produciendo una sombra del vector B que se reposa sobre el vector A. Esa sombra será la proyección de B sobre A. Es decir; la sombra será igual a la distancia que existe entre el punto M y O. En otras palabras: Proyección de B sobre A=OM. Observe que OM es el cateto adyacente del triángulo rectángulo OMB, y por trigonometría sabemos que el cateto adyacente del triángulo se puede determinar por medio de una razón trigonométrica, la cual es: 

Fórmula 1: Razón trigonométrica coseno.

Si queremos saber quién es OM, habrá que despejarlo de la fórmula 1; por ello OM quedará como:

Cateto adyacente del triángulo rectángulo OMB.

Y por consiguiente, OM será la proyección de B sobre A.

Entonces; acorde a la definición 1, se tendrá la siguiente igualdad:

A°B=lAllOMl

Ecuación 1. Producto punto de A°B usando el cateto adyacente de teta.

Sin embargo; como acabamos de ver, lOMl es la magnitud de lBl multiplicado por el coseno del ángulo entre los vectores A y B. Por lo que si queremos expresar la ecuación 1 en términos de A, B y teta, tendríamos que sustituir lOMl por lBlcos(teta) en la ecuación 1, llegando así a la ecuación mostrada en la "Definición 10.6."

¿Qué pasa si en lugar de A°B se tiene B°A?

Para B°A nos enfrentamos al siguiente dilema que se concentra en las siguientes dos preguntas:

1) ¿Será la magnitud de B multiplicada por la proyección de A sobre B?

Dado que la proyección de B sobre A mostrada en la gráfica 1, responde a la pregunta:  "¿qué tanto de la <<sombra>> de B se encuentra en A?" Y la respuesta fue la longitud OM que es igual a la magnitud del vector B por el coseno del ángulo entre los dos vectores.

Siguiendo esta misma analogía, para la solución de este caso, se tendría la siguiente pregunta: "¿qué tanto de la <<sombra>> de A se encuentra en el vector B?" 

Para responder a esta pregunta, ahora imagine que la lámpara se encuentra por debajo del vector A y que la sombra de A realiza un ángulo recto respecto a la dirección del vector B; es decir, que la sombra de A podrá apreciarse en toda la dirección de B. Téngase en consideración que el ángulo recto que formó el triángulo OMB ahora se encontrará sobre la dirección de B.

No resulta complicado dictaminar que B se encuentra cubierto totalmente por la sombra de A. O bien, para comprender mejor esta situación, se plantea la siguiente pregunta: ¿ qué tanto de A se encuentra sobre B?

Dado que lAl > lBl, la proyección de A sobre B dará como resultado una proyección igual a B, en donde ahora el ángulo recto se tendrá en el punto final que define a B, tal como se muestra en la siguiente imagen:

Gráfica 2: Proyección de A sobre B.

En la imagen se puede observa que la <<sombra>>  de A alcanza a cubrir en su totalidad al vector B. Por lo tanto el nuevo triángulo rectángulo que definirá esta proyección estará dado por el triángulo: OMB, en donde el resultado de esta proyección será igual a la magnitud de B ya que es el concepto que responde las preguntas anteriores.

Por lo tanto:

B°A= (La magnitud de B)(La proyección de A sobre B)

B°A=lBllBll

Como resultado final se tendría:

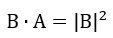Formula 2: B°A usando el concepto: "Proyección de A sobre B".

2) ¿Será la magnitud de B multiplicada por la proyección de A en la dirección de B? 

En este caso no vamos a tomar en cuenta el triángulo OMB, sino el triángulo OAK. Como se muestra en la imagen: 

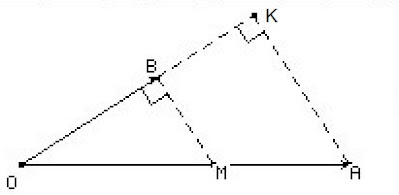Gráfica 3: Proyección de A en la dirección de B.

El triángulo OAK responde a la siguiente pregunta: ¿Qué tanto de A se encuentra proyectado sobre la dirección del vector B? O bien: ¿Qué tanto de A se encuentra en la dirección de B?

Es posible contestar a estas preguntas utilizando razones trigonométricas para descubrir ahora la longitud del lado OK del triángulo rectángulo OAK.

Si posicionamos nuestro ángulo teta sobre el vértice O, entre los vectores A y B (ver gráfica 4), el lado OK será el lado adyacente del triángulo, el lado OA será la hipotenusa del triángulo.

 

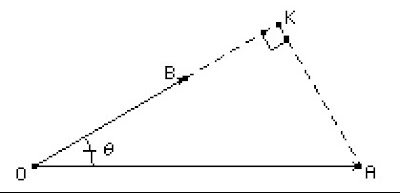Gráfica 4: Triángulo OAK.

Por tanto, la razón trigonométrica indicada para descubrir el lado OK será:

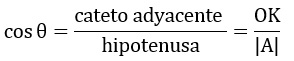Fórmula 3: coseno de teta del triángulo OAK.

 

Por lo que la distancia OK será igual a:

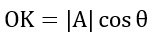Cateto adyacente del triángulo OAK.

 

 

 

Ahora que ya sabemos cuánto es esta distancia, podremos realizar la operación B punto A, la cual se expresa a continuación:

Fórmula 4: B°A usando el concepto de "...proyección sobre la dirección de B".

 

Dado que el orden de los factores no altera el producto, en este inciso 2; estaríamos afirmando que el producto punto de dos vectores que comparten el mismo punto inicial es conmutativo.  

 

Esto es:

 

Producto punto conmutativo.

 Ahora que terminamos de desarrollar los dos incisos, nos encontramos con el dilema de dictaminar cuál de los dos incisos es el correcto.

 

A continuación se enuncia la respuesta:

Los dos incisos son correctos, las operaciones realizadas en cada uno de los incisos son las descripciones puntuales de convertir el lenguaje común (con palabras) al lenguaje matemático (símbolos y números). 

Por tanto, si utilizamos con palabras el concepto de "...proyección en dirección de..." nos ubicaremos en el segundo inciso y podremos afirmar que bajo este lenguaje descrito con palabras, el producto punto es conmutativo.

Por el contrario, si con palabras, utilizamos el concepto de "...proyección de A sobre B" , nos encontraremos que el producto punto de dos vectores que comparten punto inicial y que dichos vectores tienen magnitudes distintas, no será conmutativo.

 

Aunque en el ámbito académico, el producto punto se utiliza como se muestra en el inciso dos (con su propiedad conmutativa), es de notar que algunos profesores y autores, utilizan la descripción que se enuncia con palabras en el inciso uno, generando así una descripción no puntual entre el lenguaje común y matemático.

Por ello, se extiende la invitación a profesores y autores a emplear la descripción con palabras enunciada en el inciso dos de esta publicación, para generar una descripción más acertada y puntual entre lenguaje común y matemático.

Referencias y bibliografía:

(1) Fuller Gordon, Geometría Analítica, Grupo Patria Cultural, 5° Edición, p. 299. (2001)