Ecuación general de la Elipse.

 La ecuación general de la elipse parte de la ecuación general de segundo grado, la cual se muestra a continuación:

Ecuación general de segundo grado.

Donde A, B, C, D, E, y F, son los coeficientes de la ecuación y son números pertenecientes al conjunto de los números reales. De tal forma que dependiendo del valor de sus coeficientes es como podremos clasificar la ecuación en alguna de las cuatro cónicas que se pueden formar cortando un cono recto a través de un plano. 

En el caso particular de la ecuación de una elipse, el plano que cortará al cono deberá tener una cierta inclinación respecto al eje horizontal, formándose una elipse en la superficie del plano que corta al cono recto. Tal como se puede apreciar en la siguiente imagen:

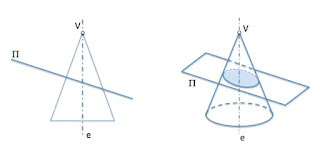Plano inclinado cortando un cono recto. (1)

La ecuación general de una elipse involucra todos los posibles casos que puedan describir una elipse, entre ellos encontramos tres clases de elipses las cuales se enuncian a continuación:

1. Elipses con centro en el origen.
2. Elipses con centro en el punto (h,k)
3. Elipses rotadas con centro en (h,k) o en el origen.

Cada caso cuenta con su respectiva ecuación y sin embargo la ecuación general de segundo grado, puede describir cualquiera de estos casos, dependiendo del valor de los coeficientes de la ecuación. 

Por ejemplo:

1. Si B, D y E son cero, F menor que cero, A y C tienen el mismo signo, son mayores que cero y A es diferente de C, entonces, la ecuación describe el primer caso.
   
2. Si B=0, A y C poseen el mismo signo y tienen valores distintos, D, E y F son diferentes de cero, la ecuación podría describir una elipse del caso 2.
3. Si B es diferente de cero; A y C poseen el mismo signo y tienen valores distintos entre sí, D, E, son diferentes de cero y F adopta cualquier valor real; entonces podría tratarse de una elipse ubicada en el caso 3.

Decimos "podría" porque hace falta un análisis profundo de la ecuación para dictaminar la veracidad de que la ecuación describa una elipse que se encuentre en cualquiera de los tres casos enunciados anteriormente. Ya que algunas veces, una ecuación puede presentar las características antes descritas y resultar ser un punto en el espacio, una recta, dos rectas o no tener gráfica.

 Referencias:

(1) Imagen tomada de: PIZiadas

Bibliografía:

Fuller Gordon, Geometría Analítica, CECSA, 5th edición, páginas: 141-153.